The other day I was pondering the prevalence of single-method interfaces (SMI) in Go, and what makes them so practical and helpful. SMIs have proven to be a very successful software modeling tool for Go programmers, and you find them all over Go code-bases.

I tried to think about the fundamentals, which brought me to some of the earliest roots of our trade: functional programming and higher-order functions (HOF). I discussed some examples of applying higher-order functions in Go recently.

This post will describe how SMIs are a more general and powerful technique than HOFs. It makes the following claims:

1. SMIs can do whatever HOFs can
2. SMIs are more general
3. SMIs are somewhat more verbose for simple cases

To begin, let’s use the same example as before.

The tree search example using SMIs

The previous post demonstrated a Go solution using higher-order functions for the tree search problem described earlier. I encourage you to review the earlier posts to get the most out of this one.

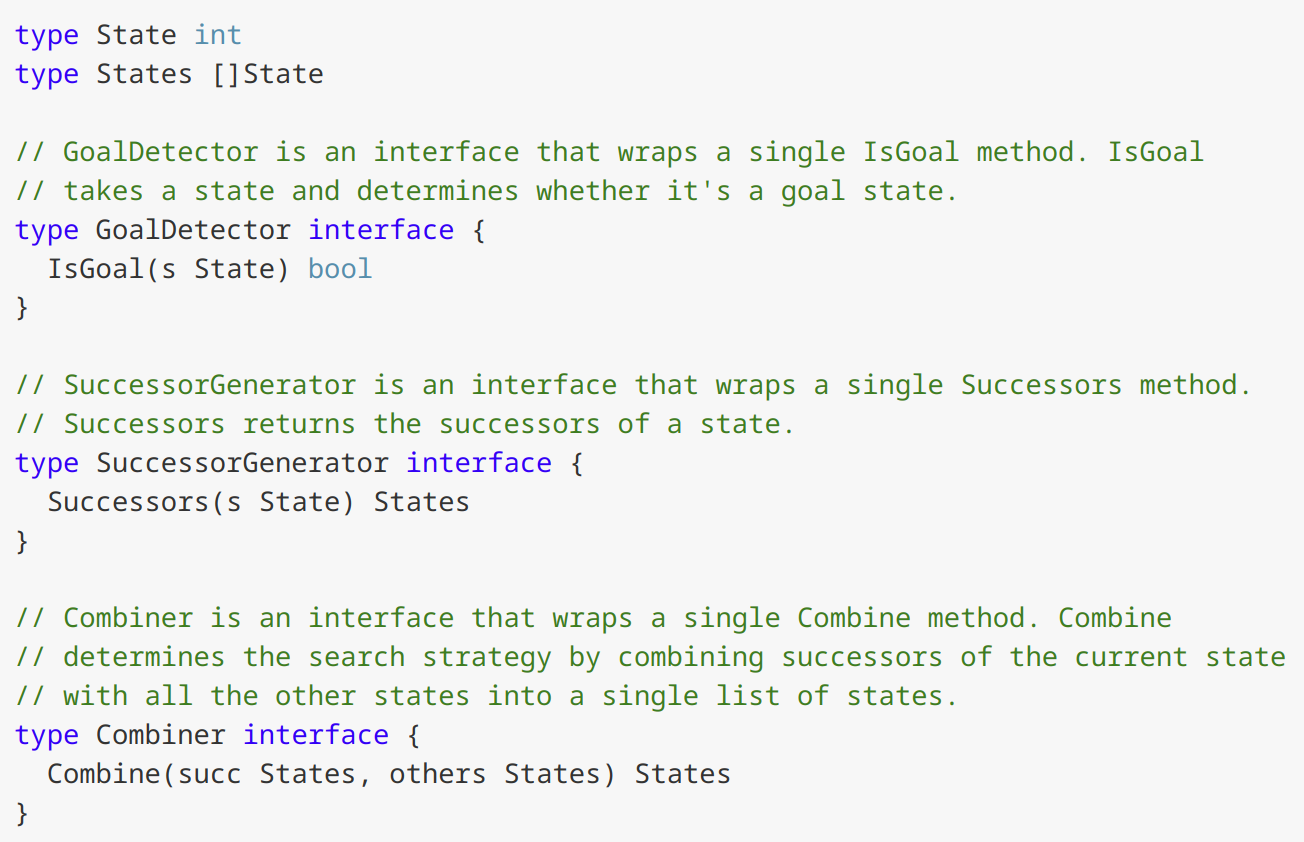
Let’s see how the same task can be accomplished using SMIs instead of HOFs; the full code is on GitHub. Starting with the types:

type State int
type States []State

// GoalDetector is an interface that wraps a single IsGoal method. IsGoal
// takes a state and determines whether it's a goal state.
type GoalDetector interface {
  IsGoal(s State) bool
}

// SuccessorGenerator is an interface that wraps a single Successors method.
// Successors returns the successors of a state.
type SuccessorGenerator interface {
  Successors(s State) States
}

// Combiner is an interface that wraps a single Combine method. Combine
// determines the search strategy by combining successors of the current state
// with all the other states into a single list of states.
type Combiner interface {
  Combine(succ States, others States) States
}

These are the equivalent SMIs to the GoalP, Successors and Combiner function types we’ve seen before; the names are slightly modified to be more suitable for interfaces and their methods.

The tree search itself – using these interfaces – is almost identical to the previous version:

func treeSearch(states States, gd GoalDetector, sg SuccessorGenerator, combiner Combiner) State {
  if len(states) == 0 {
    return -1
  }

  first := states[0]
  if gd.IsGoal(first) {
    return first
  } else {
    return treeSearch(combiner.Combine(sg.Successors(first), states[1:]), gd, sg, combiner)
  }
}

To implement BFS, we reuse prependOthers from the previous post (it remains identical):

And again, appendOthers and implementing DFS:

func bfsTreeSearch(start State, gd GoalDetector, sg SuccessorGenerator) State { return treeSearch(States{start}, gd, sg, CombineFunc(prependOthers)) }